第23条

クルマを知ること物理的思考

クルマは地球上の物理学的法則に支配されるもの。ドリフトも物理学？

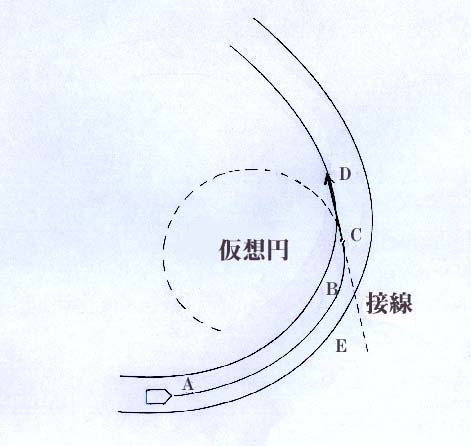クルマを減速させる操作方法はふたつ。ブレーキペダルを踏み込むこと、アクセルペダルから足を離すことだ。アクセルペダルから足を離した状態をエンジンブレーキと呼ぶことは運転免許証を持っていれば誰でも知っているね。それではこのふたつの方法で必ずクルマは減速するのだろうか？ 　話を元に戻そう。スリップに驚いたドライバーは減速するためにアクセルを戻し、ブレーキペダルを踏み込んだ。とたんにクルマはスピンして路肩に一直線。防音壁に後ろ向きに激突してしまった。ドライバーは何が起こったのか全くわからない。 　場所は緩い左コーナーだった。アクセルを抜いた瞬間にテールが右側にスライドし、クルマは進行方向に対して左側を向きはじめた。そこでブレーキングしたため、左前方の路肩に向かって一直線に進んでしまった。（右図参照） 　左コーナーなのだから普通に考えれば進行方向の右側、つまりコーナーのアウト側にぶつかってしまうような気がするだろう。ところが実際にはコーナーのイン側にぶつかってしまったのだ。原因はドライバーの操作にある。右図を見ながら説明すると、Ａ地点でスリップが発生してからＢ地点まではクルマのコーナリングラインはカーブに一致していたのだが、アクセルが完全オフになったＢ地点からＣ地点まではコーナリング半径が小さくなって（アクセルオフによってコーナリング半径を小さくするテクニックをタックインという）しまった。その後ブレーキングしたＣ地点でクルマは一気にコントロール不能となって矢印方向に行ってしまったのである。この図の中でＡ、Ｂ、Ｃがそれぞれ離れているのは、クルマには空走時間があるからだ。わかるかな？ 　アクセルペダルから足を離してエンジン回転が落ち始めるまでの間にクルマが進む距離がＡからＢまで、ブレーキペダルに足がのって４輪のタイヤに制動がかかるまでの間にクルマが進む距離がＢからＣまでということだよ。そして大切なのがＣ地点からＤ地点まで一直線に進んでしまうことだ。これは図中にあるようにＢからＣ地点までのコーナリング半径によって描かれる仮想円のＣ地点における接線なんだ。物理の教科書を開けばこの意味がわかるのだけど。 　ここで問題をひとつ。Ａ地点からＤ地点の間で、タイヤが完全にグリップを失っているのはどこの区間か？　よ〜く考えてから次に進んでね。24条ではちょっと予習しておこうか。

ドラテク皆伝第22条

ドラテク皆伝第24条

ドラテク皆伝ＩＮＤＥＸ（序章）に戻る

ドライビングテクニック皆伝

「レイテック」トップに戻る